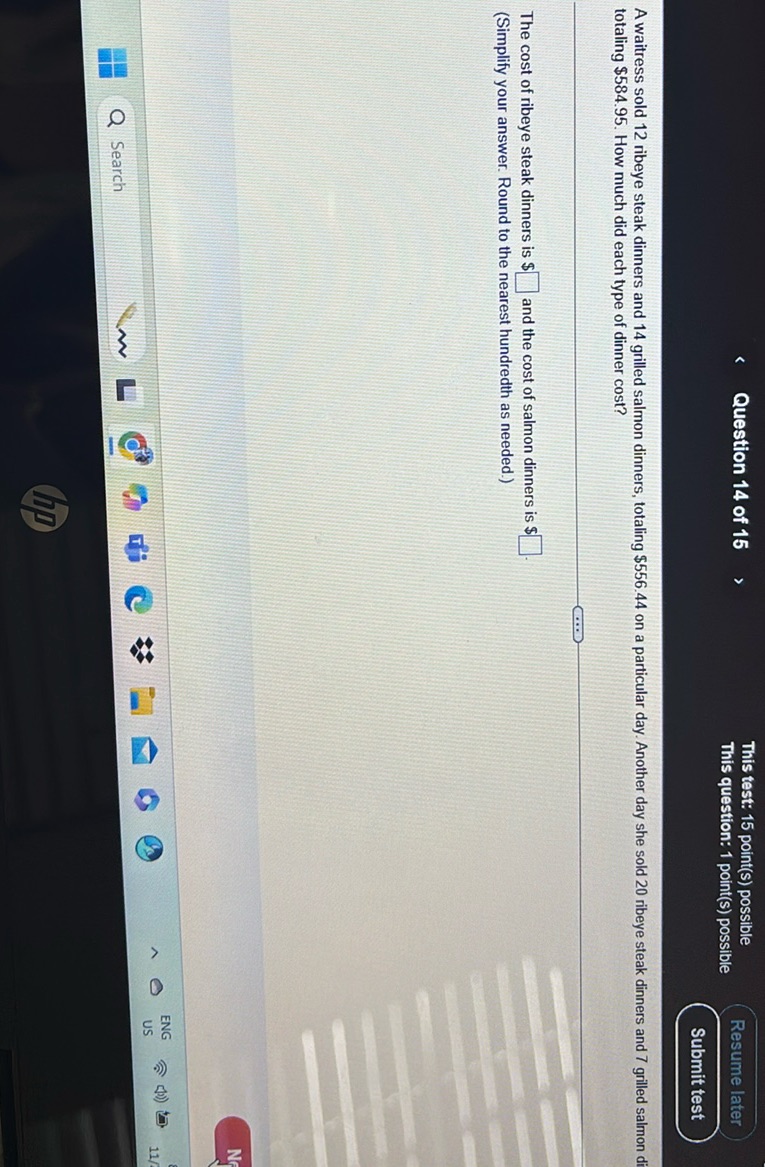
Question: A waitress sold 12 ribeye steak dinners and 14 grilled salmon dinners, totaling $556.44 on a…

A waitress sold 12 ribeye steak dinners and 14 grilled salmon dinners, totaling $556.44 on a particular day. Another day she sold 20 ribeye steak dinners and 7 grilled salmon dinners, totaling $584.95. How much did each type of dinner cost?

The cost of ribeye steak dinners is $ \boxed{\phantom{00}} $ and the cost of salmon dinners is $ \boxed{\phantom{00}} $.

(Simplify your answer. Round to the nearest hundredth as needed.)

Solution

To solve the problem, let’s set up the following equations based on the information given: Let \( x \) be the cost of a ribeye steak dinner and \( y \) be the cost of a grilled salmon dinner. From the first day: \[ \begin{cases} 12x + 14y = 558.95 & \\ 20x + 7y = 355.04 & \end{cases} \] Let’s solve this system of equations. Start with the first equation: \[ 12x + 14y = 558.95 \] and the second equation: \[ 20x + 7y = 355.04 \] Multiply the second equation by 2 to align the coefficients of \( y \): \[ 40x + 14y = 710.08 \] Subtract the first equation from this new equation: \[ \begin{align*} (40x + 14y) - (12x + 14y) &= 710.08 - 558.95 \\ 28x &= 151.13 \end{align*} \] Solve for \( x \): \[ x = \frac{151.13}{28} \approx 5.40 \] Now substitute \( x = 5.40 \) back into the first equation to find \( y \): \[ 12(5.40) + 14y = 558.95 \] \[ 64.8 + 14y = 558.95 \] Subtract 64.8 from both sides: \[ 14y = 494.15 \] Solve for \( y \): \[ y = \frac{494.15}{14} \approx 35.30 \] So, the cost of a ribeye steak dinner is approximately $5.40, and the cost of a salmon dinner is approximately $35.30.