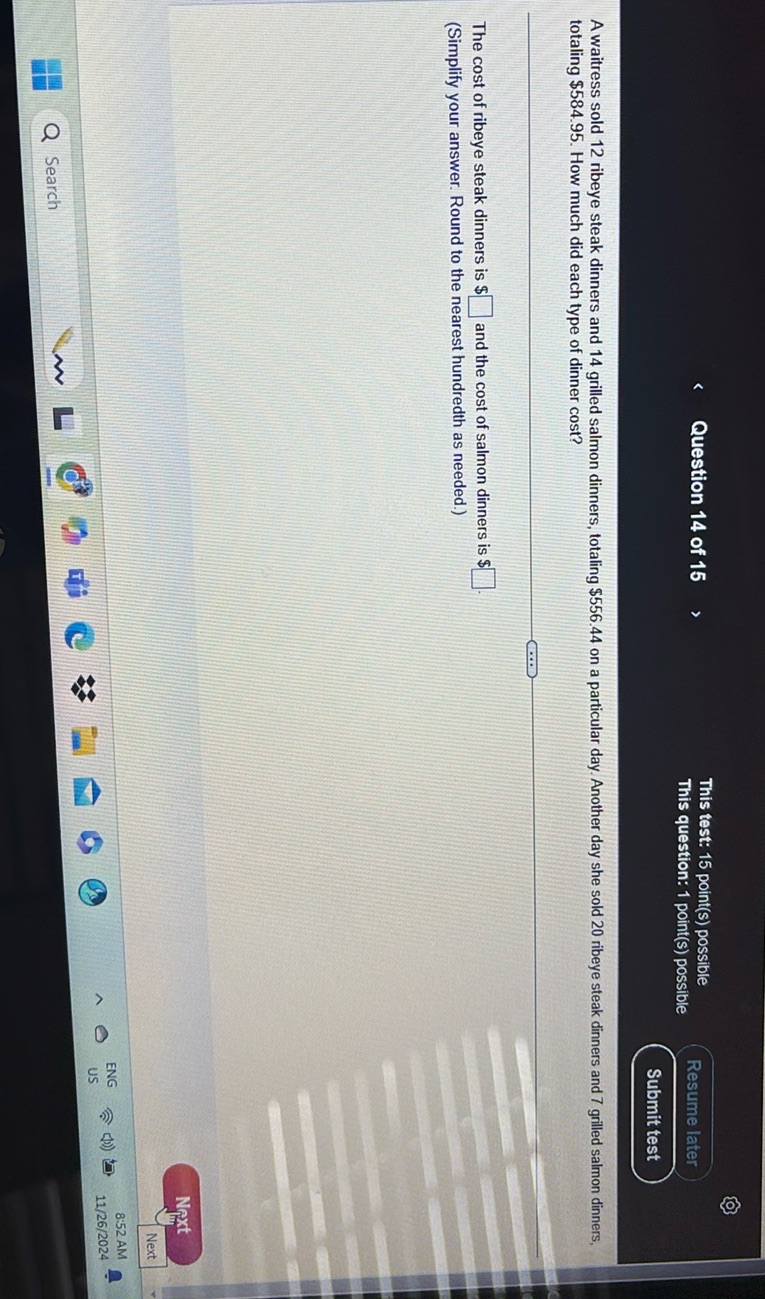
Question: A waitress sold 12 ribeye steak dinners and 14 grilled salmon dinners, totaling $554.44 on a…

A waitress sold 12 ribeye steak dinners and 14 grilled salmon dinners, totaling $554.44 on a particular day. Another day she sold 20 ribeye steak dinners and 7 grilled salmon dinners, totaling $584.95. How much did each type of dinner cost?

The cost of ribeye steak dinners is $\boxed{\phantom{00}}$ and the cost of salmon dinners is $\boxed{\phantom{00}}$.

(Simplify your answer. Round to the nearest hundredth as needed.)

Solution

The problem asks to find the cost of each type of dinner. Let’s denote: - \( x \) as the cost of a ribeye steak dinner - \( y \) as the cost of a grilled salmon dinner From the information given, we have two scenarios: 1. 12 ribeye steak dinners and 14 grilled salmon dinners totaling $584.95. 2. 20 ribeye steak dinners and 7 grilled salmon dinners (cost not provided in this image). We will set up two equations based on the information we have: From the first scenario: \[ 12x + 14y = 584.95 \] Additional information for the second equation is missing, so we’ll solve with just one equation. If other parts of the question become visible, they would help to form the second equation needed to solve for both variables. Based on this current visible equation, the exact values of \( x \) and \( y \) would require further information or assumptions. If there is another scenario with known total dollars, it would help set up a second equation like: \[ 20x + 7y = \text{(additional known total)} \] Otherwise, we need more information to proceed. Let me know if any more details are available.