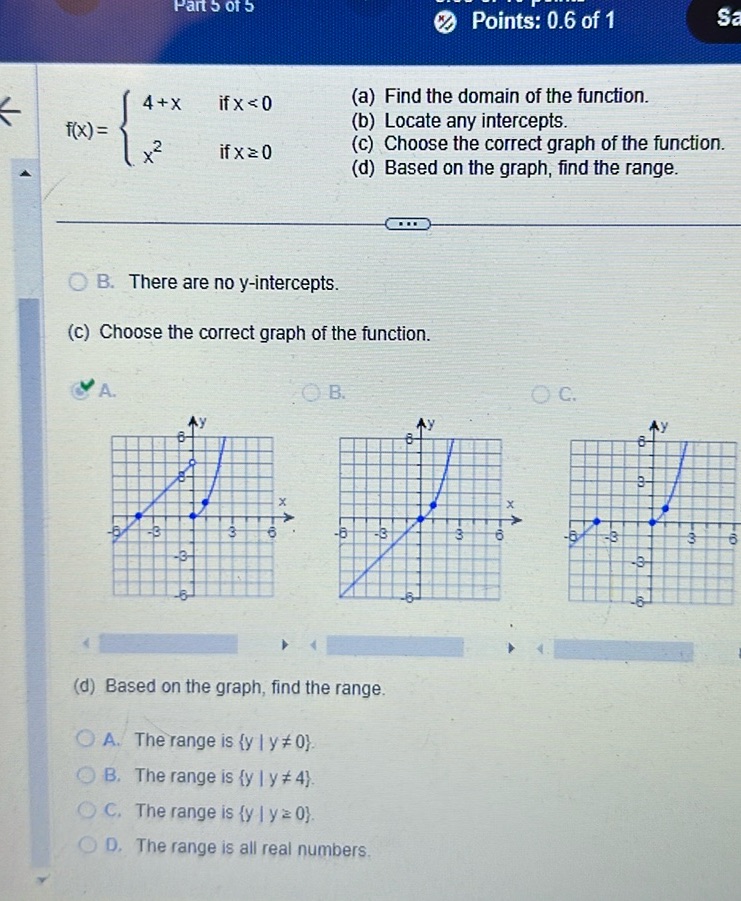
Question: (a) Find the domain of the function. (b) Locate any intercepts. (c) Choose the correct graph of the…

(a) Find the domain of the function. (b) Locate any intercepts. (c) Choose the correct graph of the function. (d) Based on the graph, find the range.

f(x) = \[ \begin{cases} 4 + x & \text{if } x < 0 \\ x^2 & \text{if } x \geq 0 \end{cases} \]

(c) Choose the correct graph of the function.

A. There are no y-intercepts.

A. \[ \text{Graph A} \] B. \[ \text{Graph B} \] C. \[ \text{Graph C} \]

(d) Based on the graph, find the range.

A. The range is \{y | y ≠ 0\}. B. The range is \{y | y ≠ 4\}. C. The range is \{y | y ≥ 0\}. D. The range is all real numbers.

Solution

(a) Find the domain of the function. For the piecewise function \( f(x) \): \[ f(x) = \begin{cases} 4 + x & \text{if } x < 0 \\ x^2 & \text{if } x \geq 0 \end{cases} \] The domain is all real numbers, \( x \in \mathbb{R} \). (b) Locate any intercepts. The y-intercept occurs where the function crosses the y-axis, i.e., when \( x = 0 \). \[ f(0) = 0^2 = 0 \] The y-intercept is at \( (0, 0) \). (c) Choose the correct graph of the function. Based on the piecewise function: - For \( x < 0 \), the linear function \( 4 + x \) decreases linearly. - For \( x \geq 0 \), the quadratic function \( x^2 \) forms a parabola opening upwards. The correct graph corresponds to graph A. (d) Based on the graph, find the range. The range from graph A is \( y \geq 0 \) since the quadratic part starts at the origin and goes upwards. The range is \( \{ y \mid y \geq 0 \} \).