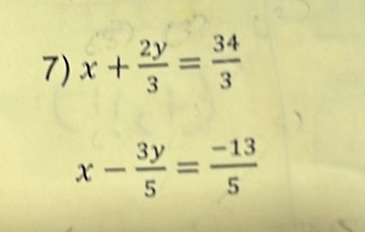
Question: 7) \( x + \frac{2y}{3} = \frac{34}{3} \) \( x - \frac{3y}{5} = \frac{-13}{5} \)

7. \( x + \frac{2y}{3} = \frac{34}{3} \)

\( x - \frac{3y}{5} = \frac{-13}{5} \)

Solution

To solve the system of equations, we first rewrite the equations without fractions. The original system is: \[ \begin{cases} x + \frac{2y}{3} = \frac{34}{3} & \\ x - \frac{3y}{5} = \frac{-13}{5} & \end{cases} \] Step 1: Eliminate the fractions in the first equation. Multiply every term by 3: \[ 3x + 2y = 34 \] Step 2: Eliminate the fractions in the second equation. Multiply every term by 5: \[ 5x - 3y = -13 \] Now we have a new system of equations: \[ \begin{cases} 3x + 2y = 34 & \\ 5x - 3y = -13 & \end{cases} \] Step 3: Solve for one variable. Let’s solve for \(x\) using the first equation. From the first equation: \[ 3x + 2y = 34 \] Solve for \(x\): \[ 3x = 34 - 2y \] \[ x = \frac{34 - 2y}{3} \] Step 4: Substitute \(x\) in the second equation. Substitute \(x = \frac{34 - 2y}{3}\) into the second equation: \[ 5\left(\frac{34 - 2y}{3}\right) - 3y = -13 \] Clear the fraction by multiplying every term by 3: \[ 5(34 - 2y) - 9y = -39 \] Distribute 5: \[ 170 - 10y - 9y = -39 \] Combine like terms: \[ 170 - 19y = -39 \] Step 5: Solve for \(y\). Subtract 170 from both sides: \[ -19y = -39 - 170 \] \[ -19y = -209 \] Divide both sides by -19: \[ y = \frac{-209}{-19} \] \[ y = 11 \] Step 6: Solve for \(x\) using the value of \(y\). Substitute \(y = 11\) back into \(x = \frac{34 - 2y}{3}\): \[ x = \frac{34 - 2(11)}{3} \] \[ x = \frac{34 - 22}{3} \] \[ x = \frac{12}{3} \] \[ x = 4 \] The solution to the system of equations is \(x = 4\) and \(y = 11\).