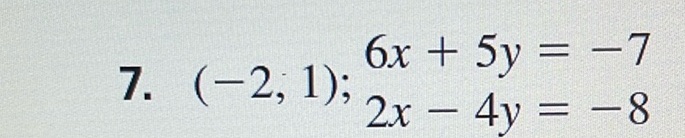
Question: 7. \((-2, 1)\); \(\frac{6x + 5y = -7}{2x - 4y = -8}\)

Solution

To solve the system of equations: \[ \begin{cases} 6x + 5y = -7 & \\ 2x - 4y = -8 & \end{cases} \] We can use the substitution method to verify if the point \((-2, 1)\) is a solution. Substitute \(x = -2\) and \(y = 1\) into the first equation: \[ 6(-2) + 5(1) = -7 \] Calculate: \[ -12 + 5 = -7 \] The equation holds, so the point satisfies the first equation. Now substitute \(x = -2\) and \(y = 1\) into the second equation: \[ 2(-2) - 4(1) = -8 \] Calculate: \[ -4 - 4 = -8 \] The equation holds, so the point also satisfies the second equation. Therefore, the point \((-2, 1)\) is a solution to the system of equations.