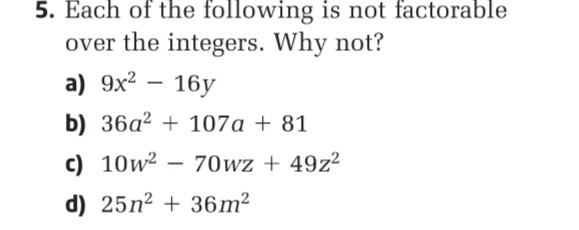
Question: 5. Each of the following is not factorable over the integers. Why not? a) $9x^2 - 16y$ b) $36a^2…

5. Each of the following is not factorable over the integers. Why not?

a) $9x^2 - 16y$

b) $36a^2 + 107a + 81$

c) $10w^2 - 70wz + 49z^2$

d) $25n^2 + 36m^2$

Solution

a) To determine why \( 9x^2 - 16y \) is not factorable over the integers: The expression resembles a difference of squares, which factors as \( a^2 - b^2 = (a - b)(a + b) \). However, for \( 9x^2 - 16y \) to be factorable in integers, both \( 9x^2 \) and \( 16y \) must be perfect squares with integer coefficients. Since \( 16y \) is only a perfect square if \( y \) is a perfect square, and there is no guarantee that \( y \) is a perfect square, the expression cannot be factored over the integers. \[ 9x^2 - 16y \] b) To determine why \( 36a^2 + 107a + 81 \) is not factorable over the integers: For a quadratic expression \( ax^2 + bx + c \) to be factorable over the integers, the discriminant \( b^2 - 4ac \) must be a perfect square. Calculating the discriminant: \[ b^2 - 4ac = 107^2 - 4 \times 36 \times 81 = 11449 - 11664 = -215 \] Since the discriminant is negative, there are no real roots, and thus the quadratic cannot be factored over the integers. \[ 36a^2 + 107a + 81 \] c) To determine why \( 10w^2 - 70wz + 49z^2 \) is not factorable over the integers: Assume the expression can be factored as \( (mw + nz)(pw + qz) \). Expanding: \[ mw \times pw + mw \times qz + nz \times pw + nz \times qz = mpw^2 + (mq + np)wz + nqz^2 \] Comparing coefficients: \[ mp = 10 \] \[ mq + np = -70 \] \[ nq = 49 \] Looking for integer pairs that satisfy \( mp = 10 \) and \( nq = 49 \): Possible pairs for \( (m, p) \): (1,10), (2,5), (5,2), (10,1) Possible pairs for \( (n, q) \): (1,49), (7,7), (49,1) Testing these combinations does not yield integer solutions that satisfy \( mq + np = -70 \). Therefore, the expression cannot be factored over the integers. \[ 10w^2 - 70wz + 49z^2 \] d) To determine why \( 25n^2 + 36m^2 \) is not factorable over the integers: The expression is a sum of squares, which does not factor over the integers. For it to be factorable, it would need to be expressed as \( (an + bm)(cn + dm) \). However, expanding such a product does not yield a sum of squares. Thus, \( 25n^2 + 36m^2 \) cannot be factored over the integers. \[ 25n^2 + 36m^2 \]