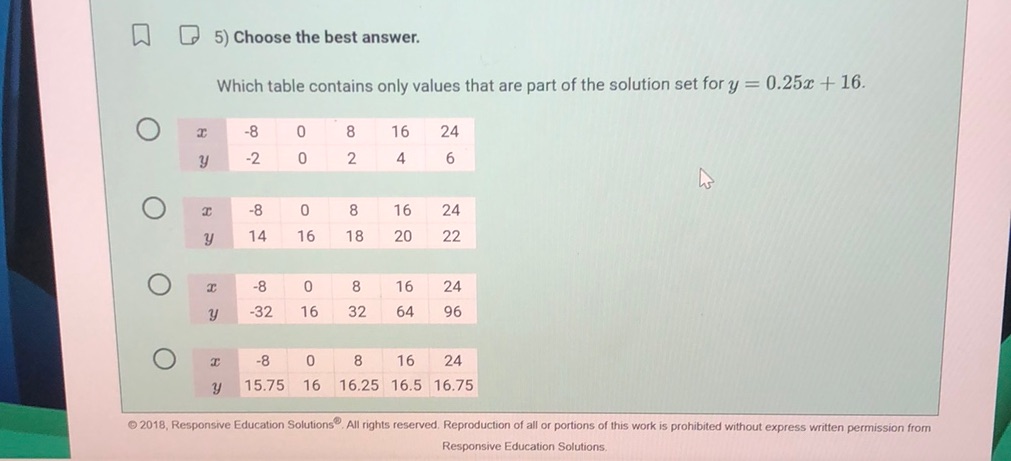
Question: 5) Choose the best answer. Which table contains only values that are part of the solution set for…

5. Choose the best answer.

Which table contains only values that are part of the solution set for \( y = 0.25x + 16 \)?

\[ \begin{array}{c|cccc} x & -8 & 0 & 8 & 16 \\ \hline y & -2 & 0 & 2 & 4 \end{array} \]

\[ \begin{array}{c|cccc} x & -8 & 0 & 8 & 16 \\ \hline y & 14 & 16 & 18 & 20 \end{array} \]

\[ \begin{array}{c|cccc} x & -8 & 0 & 8 & 16 \\ \hline y & -32 & 16 & 32 & 64 \end{array} \]

\[ \begin{array}{c|cccc} x & -8 & 0 & 8 & 16 \\ \hline y & 15.75 & 16 & 16.25 & 16.5 \end{array} \]

Solution

To solve this problem, we need to verify which table contains pairs \((x, y)\) that satisfy the equation \(y = 0.25x + 16\). Let’s check each option: Option 1: For \(x = -8\), calculate: \[ y = 0.25(-8) + 16 = -2 + 16 = 14 \] The given \(y\) is 8. This does not match. For \(x = 0\), calculate: \[ y = 0.25(0) + 16 = 0 + 16 = 16 \] The given \(y\) is 8. This does not match. This option does not match. Option 2: For \(x = -8\), calculate: \[ y = 0.25(-8) + 16 = -2 + 16 = 14 \] The given \(y\) is 14. This matches. For \(x = 0\), calculate: \[ y = 0.25(0) + 16 = 0 + 16 = 16 \] The given \(y\) is 16. This matches. For \(x = 16\), calculate: \[ y = 0.25(16) + 16 = 4 + 16 = 20 \] The given \(y\) is 20. This matches. For \(x = 24\), calculate: \[ y = 0.25(24) + 16 = 6 + 16 = 22 \] The given \(y\) is 22. This matches. This option matches all pairs. Option 3: For \(x = -8\), calculate: \[ y = 0.25(-8) + 16 = -2 + 16 = 14 \] The given \(y\) is -32. This does not match. This option does not match. Option 4: For \(x = -8\), calculate: \[ y = 0.25(-8) + 16 = -2 + 16 = 14 \] The given \(y\) is 15.75. This does not match. This option does not match. Therefore, the correct option is Option 2.