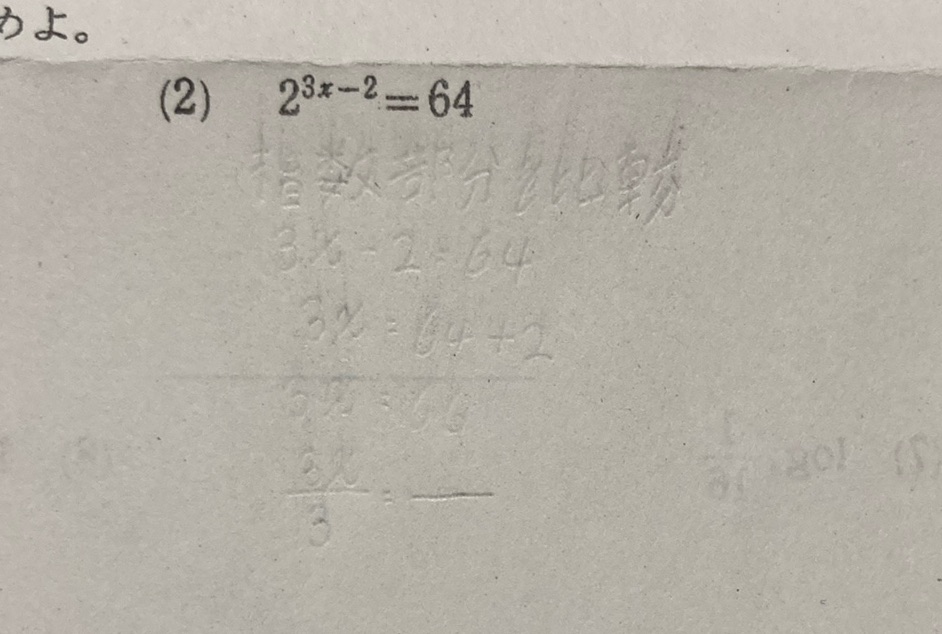
Question: (2) \(2^{3x-2} = 64\) \(3x - 2 = 64\) \(3x = 64 + 2\) \(3x = 66\) \(x =…

(2) \(2^{3x-2} = 64\)

\(3x - 2 = 64\)

\(3x = 64 + 2\)

\(3x = 66\)

\(x = \frac{66}{3}\)

Solution

The problem in the photo is: \[ 2^{3x - 2} = 64 \] Start by expressing 64 as a power of 2. We know that: \[ 64 = 2^6 \] Now, equate the exponents: \[ 3x - 2 = 6 \] Add 2 to both sides: \[ 3x = 6 + 2 \] \[ 3x = 8 \] Divide both sides by 3: \[ x = \frac{8}{3} \] Thus, the solution is: \[ x = \frac{8}{3} \]