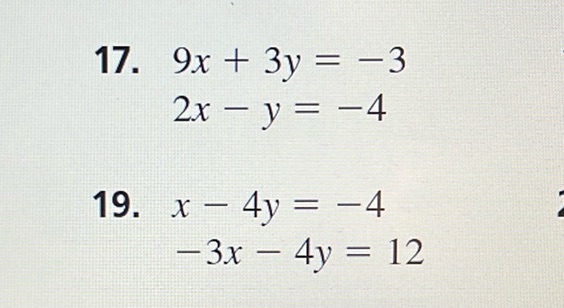
Question: 17. \[ \begin{align*} 9x + 3y &= -3 \\ 2x - y &= -4 \end{align*} \] 19. \[ \begin{align*}…

17. \[ \begin{align*} 9x + 3y &= -3 \\ 2x - y &= -4 \end{align*} \]

18. \[ \begin{align*} x - 4y &= -4 \\ -3x - 4y &= 12 \end{align*} \]

Solution

Let’s solve problem 17. We have the system of equations: \[ \begin{cases} 9x + 3y = -3 & \\ 2x - y = -4 & \end{cases} \] Step 1: Solve the second equation for \( y \). \[ 2x - y = -4 \] \[ -y = -4 - 2x \] \[ y = 2x + 4 \] Step 2: Substitute \( y = 2x + 4 \) into the first equation. \[ 9x + 3(2x + 4) = -3 \] \[ 9x + 6x + 12 = -3 \] \[ 15x + 12 = -3 \] Step 3: Solve for \( x \). \[ 15x = -3 - 12 \] \[ 15x = -15 \] \[ x = -1 \] Step 4: Substitute \( x = -1 \) back into \( y = 2x + 4 \). \[ y = 2(-1) + 4 \] \[ y = -2 + 4 \] \[ y = 2 \] The solution for the system is \( x = -1 \) and \( y = 2 \).