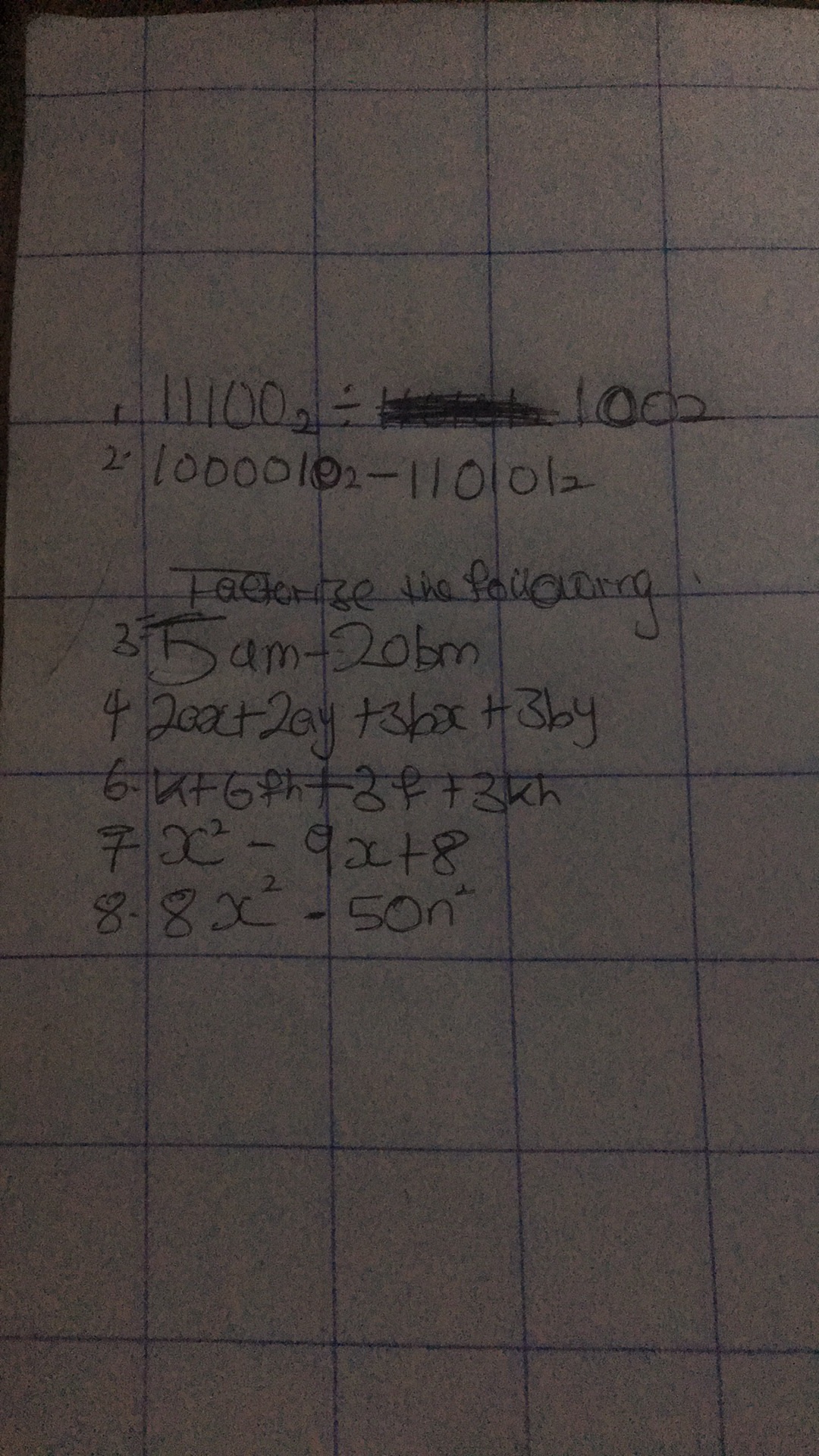
Question: 1. \(11100_2 \div 1000\) 2. \(1000010_2 - 110101_2\) Factorize the following: 3. \(5am -…

1. \(11100_2 \div 1000\)

2. \(1000010_2 - 110101_2\)

Factorize the following:

3. \(5am - 20bm\)

4. \(2ax + 2ay + 3bx + 3by\)

5. \(4t + 6th + 8t + 3kh\)

6. \(x^2 - 9x + 8\)

7. \(8x^2 - 50n^2\)

Solution

Problem 1: \(1110_2 = 1000_2\) First, convert both binary numbers to decimal. \[ 1110_2 = 1 \times 2^3 + 1 \times 2^2 + 1 \times 2^1 + 0 \times 2^0 = 8 + 4 + 2 + 0 = 14 \] \[ 1000_2 = 1 \times 2^3 + 0 \times 2^2 + 0 \times 2^1 + 0 \times 2^0 = 8 + 0 + 0 + 0 = 8 \] Since \(14 \neq 8\), the statement \(1110_2 = 1000_2\) is False. --- Problem 2: \(100001_2 - 11010_2\) First, convert both binary numbers to decimal. \[ 100001_2 = 1 \times 2^5 + 0 \times 2^4 + 0 \times 2^3 + 0 \times 2^2 + 0 \times 2^1 + 1 \times 2^0 = 32 + 0 + 0 + 0 + 0 + 1 = 33 \] \[ 11010_2 = 1 \times 2^4 + 1 \times 2^3 + 0 \times 2^2 + 1 \times 2^1 + 0 \times 2^0 = 16 + 8 + 0 + 2 + 0 = 26 \] Subtract the two decimal numbers: \[ 33 - 26 = 7 \] Convert \(7\) back to binary: \[ 7_{10} = 111_2 \] So, \[ 100001_2 - 11010_2 = 111_2 \] --- Problem 4: \(5am - 20bm\) Factor out the greatest common factor, which is \(5m\): \[ 5am - 20bm = 5m(a - 4b) \] --- Problem 5: \(2ax + 2ay + 3bx + 3by\) Group the terms: \[ 2ax + 2ay + 3bx + 3by = (2ax + 2ay) + (3bx + 3by) \] Factor out the common factors in each group: \[ = 2a(x + y) + 3b(x + y) \] Factor out \((x + y)\): \[ = (x + y)(2a + 3b) \] --- Problem 6: \(x + 6gh + 3f + 2xh\) Rearrange the terms to group like terms: \[ x + 2xh + 6gh + 3f \] Factor out the common factors: \[ = x(1 + 2h) + 3g(2h) + 3f \] However, it seems there’s a mistake in grouping. Let’s try another approach. Group \(x\) and \(2xh\), and \(6gh\) and \(3f\): \[ = x(1 + 2h) + 3(2gh + f) \] This is the factored form. --- Problem 7: \(x^2 - 9x + 8\) Find two numbers that multiply to \(8\) and add to \(-9\). These numbers are \(-1\) and \(-8\). \[ x^2 - 9x + 8 = (x - 1)(x - 8) \] --- Problem 8: \(8x^2 - 50n^2\) Factor out the greatest common factor, which is \(2\): \[ 8x^2 - 50n^2 = 2(4x^2 - 25n^2) \] Recognize the difference of squares: \[ 4x^2 - 25n^2 = (2x)^2 - (5n)^2 = (2x - 5n)(2x + 5n) \] So, the fully factored form is: \[ 8x^2 - 50n^2 = 2(2x - 5n)(2x + 5n) \]